首页 抖音真文案网文章正文

三阶矩阵运算(三阶矩阵运算公式)

抖音真文案网 2022年07月11日 13:06 118 admin

行列式这一概念，分别由日本数学家关孝和&德国数学家莱布尼茨在1683年和1693年独立提出！

根据上述定义，n阶行列式有n！项，而一个25阶行列式需要计算25！（约等于150*10⊃2;⊃3;）次乘法运算. 若一个超级计算机每秒钟能完成1万亿次乘法运算，则计算一个25阶行列式需要50万年！

一万年太久，只争朝夕！

三阶矩阵运算(三阶矩阵运算公式)

何况还是50万年~~/(ㄒoㄒ)/~~

读到这里，很多童鞋立即放弃了行列式、进而放弃了线性代数！！！

但当看到如下行列式时，这些童鞋默默地流下了眼泪.

上述行列式第一行521（wǒàinǐ），第二行125（nǐàiwǒ），第三行则是两个1314（yìshēngyíshì），更为精妙的是其结果竟然为520.

如此神级的撩妹技能，你真的不打算学学吗？

1750年，瑞士数学家克拉默给出了著名的利用行列式求解方程组的克拉默法则. 随后在1812年，法国数学家柯西给出了行列式的几何意义，揭开了其神秘的面纱，从而极大地激发了人们对行列式研究和应用的强烈兴趣.

考虑如下二阶行列式：

三阶矩阵运算(三阶矩阵运算公式)

以第一行（a，b）和第二行（c，d）为邻边构造如下平行四边形，并设OA与OB的长度分别为 r、s，且OA、OB与x轴正向夹角分别为α、β.

于是平行四边形的面积为：

综上，行列式的几何意义就是：（有向）面积. 三阶行列式的几何意义请参见《高等数学》（同济7版）下册第21页.

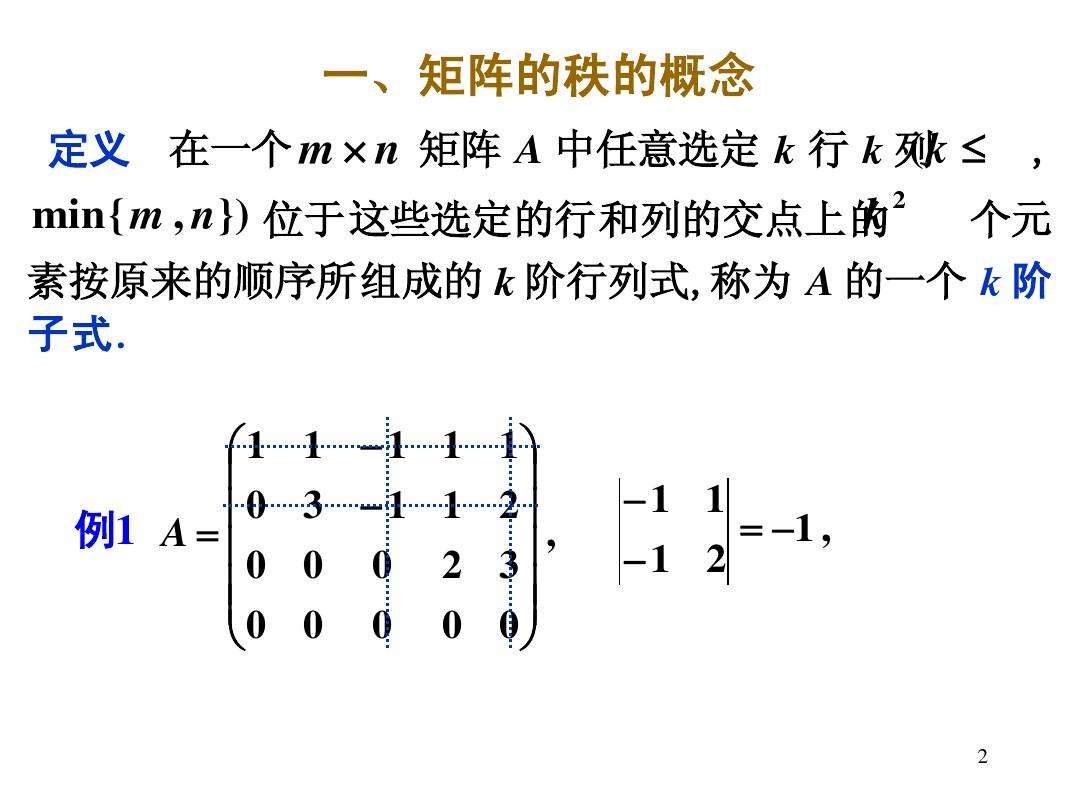
很多童鞋在初学行列式时，难免为其复杂的定义所困扰. 不过，小编可以负责任地告诉大家，关于行列式，真正重要的东东并不是那个让你烦恼的定义，而是行列式的性质及基于性质的计算.

而说到行列式的性质，你的心情是不是立马就好起来？行列式的性质十分简单易懂，无论记忆或应用都木有问题，而对于学习行列式的主要目的而言，这就够了！

一、行列式的性质

平等性：行列式的行列互换，其值不变. 这个性质告诉我们，行与列的地位是平等的；

分拆性：☜点击查看；

零化性：行向量组线性相关时，行列式为0. 特别地，含0行或某两行成比例时，行列式为0；

挖洞性：又称初等变换性，包括

互换性：互换行列式两行，其值反号；

倍乘性：行列式某一行公因数可以提出去；倍加性：将行列式某一行的倍数加到另一行，其值不变.

二、行列式的计算

超级计算机按行列式的定义计算一个25阶的行列式时需要50万年，而有了上述植树造林思想，任何普通的计算机可以在不到一秒内完成计算，这才是真正的秒杀！

行列式计算的基本方法有：

上三角化法

展开降阶法

递推公式法

行列式计算的常见技巧有：

数学归纳法

加边升阶法

分拆法

特殊公式法

三、行列式的应用

解方程组：克拉默法则

判断方阵是否可逆

判断向量组的线性相关性

计算可逆矩阵的逆矩阵

计算方阵的特征值

判断实对称矩阵是否为正定矩阵

雅可比行列式在高等数学中的应用

相关文章

发表评论

陕ICP备2022006270号-1 网站地图 抖音真文案网